Fly_Fire1000的博客

假设z轴向屏幕内，从$a_1$旋转到$a_2$，绕z轴的旋转矩阵推导(不考虑旋转正方向)：

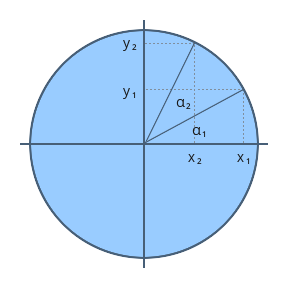
$x_1 = cos(a_1) \\ y_1 = sin(a_1) \\ x_2 = cos(a_1 + a_2) \\ y_2 = sin(a_1 + a_2)$

和角公式：

$cos(α + β) = cos \ α \cdot cos \ β - sin \ α \cdot sin \ β \\ sin(α + β) = sin \ α \cdot cos \ β + cos \ α \cdot sin \ β$

代入可得：

$x_2 = cos(a_1 + a_2) = cos \ a_1 \cdot cos \ a_2 - sin \ a_1 \cdot sin \ a_2 = x_1 \cdot cos \ a_2 - y_1 \cdot sin \ a_2 \\ y_2 = sin(a_1 + a_2) = sin \ a_1 \cdot cos \ a_2 + cos \ a_1 \cdot sin \ a_2 = y_1 \cdot cos \ a_2 +x_1 \cdot sin \ a_2$

逆推出z轴的旋转矩阵：

$\begin{bmatrix} cos \ a & - sin \ a & 0 & 0 \\ sin \ a & cos \ a & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} x \cdot cos \ a - y \cdot sin \ a \\ x \cdot sin \ a + y \cdot cos \ a \\ z \\ 1 \end{bmatrix}$

同理可推导绕y轴和x轴的旋转矩阵(不考虑旋转正方向)：

$\begin{bmatrix} cos \ a & 0 & - sin \ a & 0 \\ 0 & 1 & 0 & 0 \\ sin \ a & 0 & cos \ a & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} x \cdot cos \ a - z \cdot sin \ a \\ y \\ x \cdot sin \ a + z \cdot cos \ a \\ 1 \end{bmatrix}$

$\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & cos \ a & - sin \ a & 0 \\ 0 & sin \ a & cos \ a & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} x \\ y \cdot cos \ a - z \cdot sin \ a \\ y \cdot sin \ a + z \cdot cos \ a \\ 1 \end{bmatrix}$