《OGL dev》Etay Meiri Tutorial 13 - Camera Space 笔记
上一节中,我们假设摄影机位于原点,上方向沿着y轴正方向,朝向z轴正方向。这称为camera space或view space。
但现实中,摄影机可以位于任何位置,朝向向任何方向。因此,我们需要寻找从world space到camera space变换。这个变换称为摄影机变换或视口变换。
因为,对空间中所有对象应用相同的变换,相对位置不变。所以,我们将world space中的摄影机,应用某个变换,将摄影机变换到原点,上方向沿着y轴正方向,朝向z轴正方向,那么这个变换就是所寻找的摄影机变换。
假设world space中的摄影机的坐标为(x, y, z),应用(-x,- y,- z)平移变换,摄影机回原点。
然后可能会想再寻找一个旋转变换,将摄影机旋转到上方向沿着y轴正方向,朝向z轴正方向即可。如果camera space与world space定向相同,确实如此。但如果定向不同,就不是旋转变换力所能及的了。
UVN camera是一个方案。N表示摄影机朝向即camera space的z轴,V表示摄影机上方向,camera space的y轴,U对应camera space的x轴。UVN确定了摄影机的坐标系定向。
当已知摄影机在world space中的UVN,事实只需要知道N,在NV平面中与V同向的一个向量,world space的坐标系定向,通过叉乘就可以得到UVN。
先对UVN进行标准化,之后world space中的点点乘U就得到这个点在camera space中的x坐标,因为向量对单位向量的点乘,等于向量在这个单位向量上的投影。同理分别点乘V、N就得到camera space中的y、z坐标。也就是说,依次以U、V、N为行组成的矩阵,是从world space到camera space的变换。(因为矩阵与向量相乘时,矩阵的行与向量进行点乘)
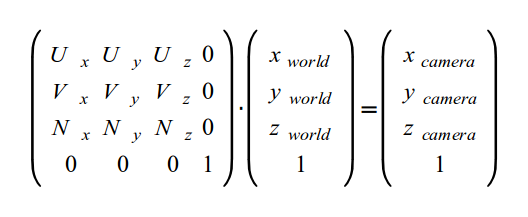
综上,先应用(-x,- y,- z)平移变换,再应用依次以U、V、N为行组成的矩阵的复合变换,就是所寻找的摄影机变换。