Fly_Fire1000的博客

Specular lighting不仅需要考虑光线强度、入射方向，还需要考虑观察者的位置。观察者处于光线反射的方向上时最亮，与反射光的夹角越大越暗。specular因子为夹角的余弦，但当夹角超过90度时，观察者接收不到反射光，specular因子为0。

specular是材质的属性。金属拥有specular属性，木头没有。

与diffuse light类似，我们需要计算每个像素的specular效果，而不只是顶点。因此，我们需要在vertex shader将顶点坐标变换到世界空间，经由光栅器插值，在fragment shader中接收到每个像素的顶点坐标。

反射光线的计算公式推导：

1. 假设入射光线为$\vec{I}$，方向从光源指向表面。$\vec{N}$是表面法线，$\vec{R}$为待求的反射光，$|\vec{I}| = |\vec{I}|$。
2. 假设从点$I$向点$R$的向量为$\vec{m}$，那么$\vec{R} = \vec{m} - \vec{I}$。
3. 因为$\vec{N}$是单位向量，所以$\vec{I} \cdot \vec{N}$是$\vec{I}$在$\vec{N}$的投影长度。假设为$\vec{n}$是$\vec{I}$在$\vec{N}$投影，那么$\vec{n} = (\vec{I} \cdot \vec{N}) \vec{N}$。
4. 绘图可知，$\vec{I} = \vec{m} / 2 + \vec{n}$。所以$\vec{m} / 2 = \vec{I} - \vec{n}$，所以$\vec{m} = 2 \vec{I} - 2 \vec{n}$。
5. 因为$\vec{n} =(\vec{I} \cdot \vec{N}) \vec{N}$，代入上式可得$\vec{m} = 2 \vec{I} - 2 (\vec{I} \cdot \vec{N}) \vec{N}$。
6. 将上式代入$\vec{R} = \vec{m} - \vec{I}$，可得$\vec{R} = 2 \vec{I} - 2 (\vec{I} \cdot \vec{N}) \vec{N} - \vec{I} = \vec{I} - 2 (\vec{I} \cdot \vec{N}) \vec{N}$。

• 入射光线为$\vec{I}$通过fragment shader中每个像素的顶点坐标减去于观察者，也就是摄影机坐标得到。

GLSL内置函数reflect计算反射光线：reflect(gDirectionalLight.Direction, Normal);。

1. 第一个参数是入射光线，方向从光源指向表面
2. 第二个参数是表面法线。

Specular lighting完整的计算公式如下图：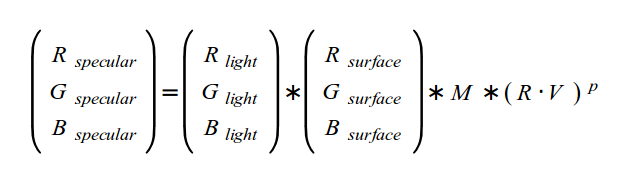

• M是材质的specular强度，比如完全没有specular属性的材质(如木头)的specular强度为0，越闪亮的材质M的值越大，比如金属。(教程中并没有说这个值的上限是1，意味着可能超过？)
• $R \cdot V$中$R$表示反射光，$V$表示从光照射表面的点到观察者的位置的向量，因为两者都是单位向量，所以$R \cdot V$就是两者夹角的余弦。
• P被称为specular power(高光指数)或shininess factor(反射因子)，作用是当specular light存在时，增加并锐化边缘。P也是材质的属性。

教程中一个模型只使用一种specular材质，是因为specular相关的属性都是应用通过uniform variable设定的。将specular相关的属性写入到vertex buffer中，可以使得一个模型不同的部分使用不同的specular材质，使用建模软件很容易实现。

在fragment shader中如果一个像素不存在diffuse light，那么就没有计算specular light必要，因为入射光线强度为0。
同理，只有specular light存在时，才需要计算specular power，也就是公式中的P。