Fly_Fire1000的博客

坐标系中，各个轴上单位向量先缩放后相加，能得到坐标系中任意向量，单位向量的缩放值就是向量对应轴上的坐标分量。

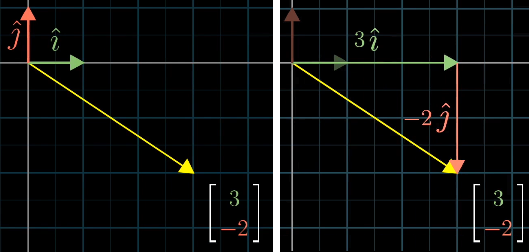
像这样，先缩放后相加能得到空间中任意向量的一组向量，称为这个空间的基，其中每一个向量称为基向量。
在二维空间中，任意两个不共线的非零向量是这个空间的基。二维空间中的任意向量，用两个基向量的缩放值表示，就是这个向量的坐标。向量的坐标取决于正在使用的基。

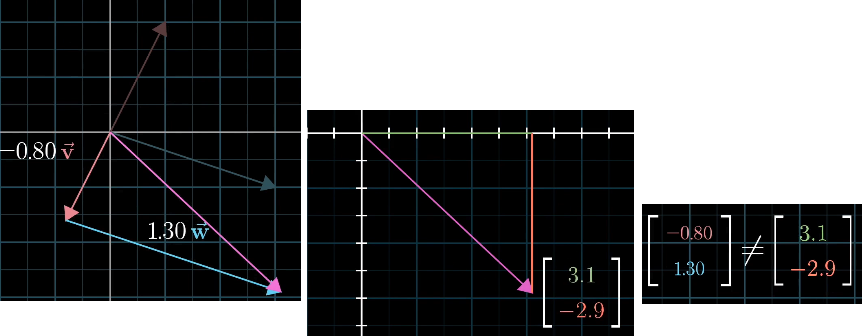
两个向量先缩放后相加的结果，被称为这两个向量的线性组合。一组向量的所有线性组合的集合，称为这组向量张成的空间(span)。

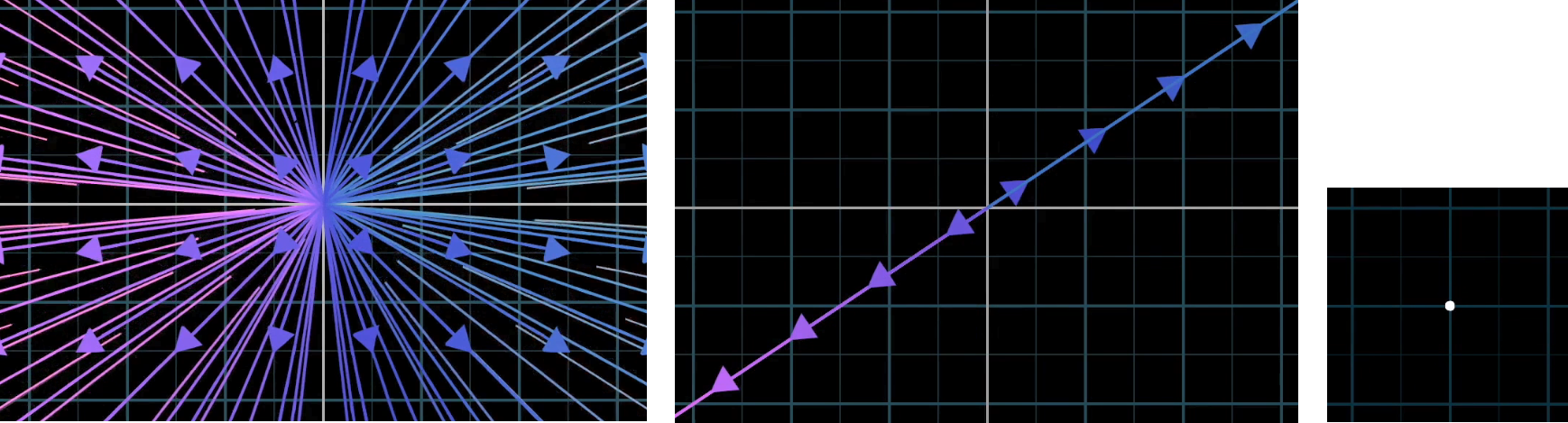
1. 两个不共线的非零二维向量张成的空间是整个二维空间。
2. 两个共线的非零二维向量张成的空间是一条过原点的直线。
3. 两个零二维向量张成的空间是原点。
   

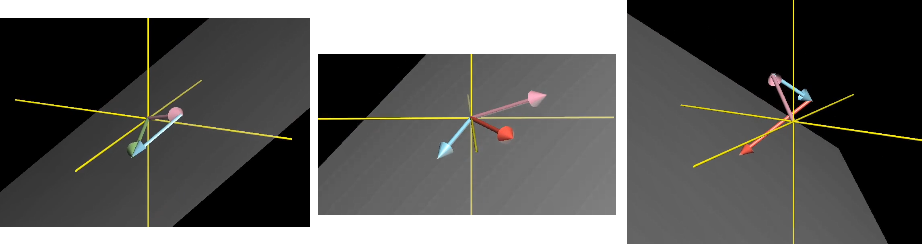
在三维空间中，两个不共线的非零三维向量张成的空间是一个过原点的平面。在这两个向量中加入一个这个平面内的三维向量，张成的空间依旧是这个平面。但加入一个这个平面外的三维向量张成的空间是整个三维空间。

一组向量，如果移除其中一个向量，不减少它们张成的空间的维度，我们称这组向量是「线性相关」的。即这组向量中存在一个向量，它可以被表示为其余向量的线性组合。
一组向量，如果移除其中一个向量，会减少它们张成的空间的维度，我们称这组向量是「线性无关」的。

张成一个空间的一组「线性无关」的向量，是这个空间的基。