《P08 线性代数的本质 - 系列合集 06 - 逆矩阵、列空间与零空间》3Blue1Brown 笔记
线性方程组如下图。
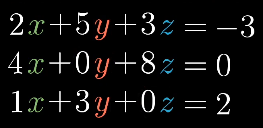
线性变换能用于解线性方程组,将解线性方程组转换为寻找目标向量。应用给定的线性变换后,结果为给定的向量,即。
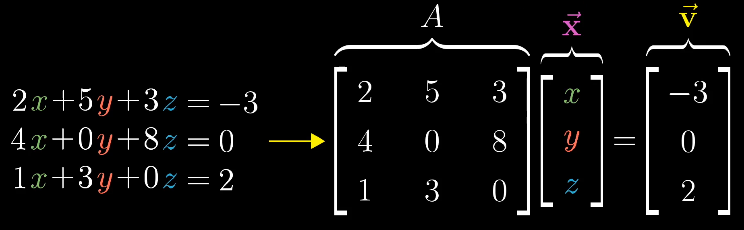
当线性变换的行列式的值不为0,即空间的维度没有被降低。那么,给定的向量应用的逆向变换,就可以得到目标向量。线性变换的逆向变换是另一个线性变换。
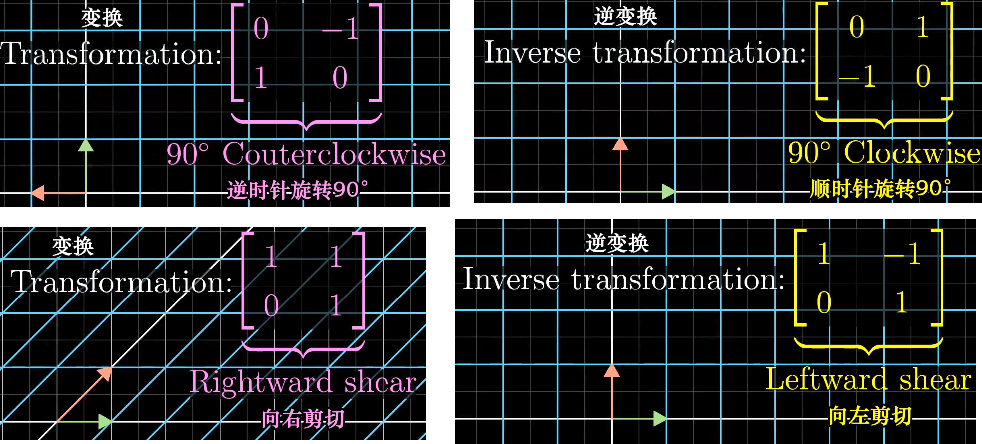
线性变换的逆向变换,称为的逆,计为。

对于,是唯一的变换,先应用,再应用,结果什么都不发生改变。因此表示什么都不做的变换,这样的变换被称为恒等变换,它的基向量变换前后保持不变。
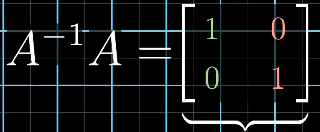
如果找到了的值(通常,通过计算机计算),在两边都乘以。因为相当于不存在,可得,即将给定向量应用,就得到了目标向量。
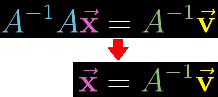
当线性变换的行列式的值为0,即空间的维度被降低。那么不存在的逆向变换,因为变换无法增加空间的维度(一个输入只对应一个输出)。这时,仅限给定向量落在变换后的空间内,目标向量存在。(不提供计算方法)
我们将一个线性变换,变换后空间的维度称为这个线性变换的「秩(Rank)」。因为变换不能增加空间的维度,所以二维矩阵的「秩」的最大值为2,小于2表示空间维度降低,这个矩阵的行列式为0。
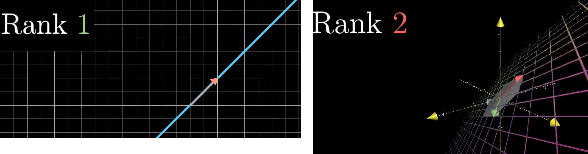
我们将一个矩阵所有变换结果的集合,称为这个矩阵的「列空间」(Column space),即矩阵的列张成的空间。「秩」就是「列空间」的维度。当一个矩阵的「秩」为最大值,等于矩阵的列数,称为「满秩」(Full Rank)。
因线性变换原点位置保持不变,零向量必定处于「列空间」中。一个「满秩」的变换,只有零向量变换后为零向量。一个非「满秩」的变换,多个向量变换为零向量。
- 「秩」为1的二维线性变换,一条直线上的向量变换为零向量。
- 「秩」为2的三维线性变换,一条直线上的向量变换为零向量。
- 「秩」为1的三维线性变换,一条平面上的向量变换为零向量。
一个矩阵,变换后落在原点的向量(零向量)的集合,称为这个矩阵的「零空间」(Null space)或「核」(Kernel)。当给定向量恰好为零向量时,「零空间」就是这个线性方向组的解。