Fly_Fire1000的博客

点积

点积的计算公式：

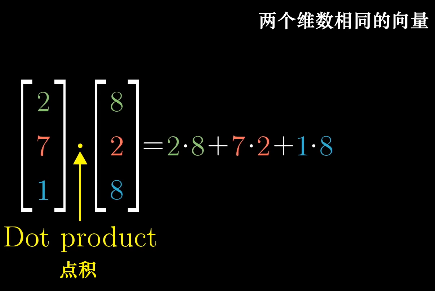
点积的几何解释：

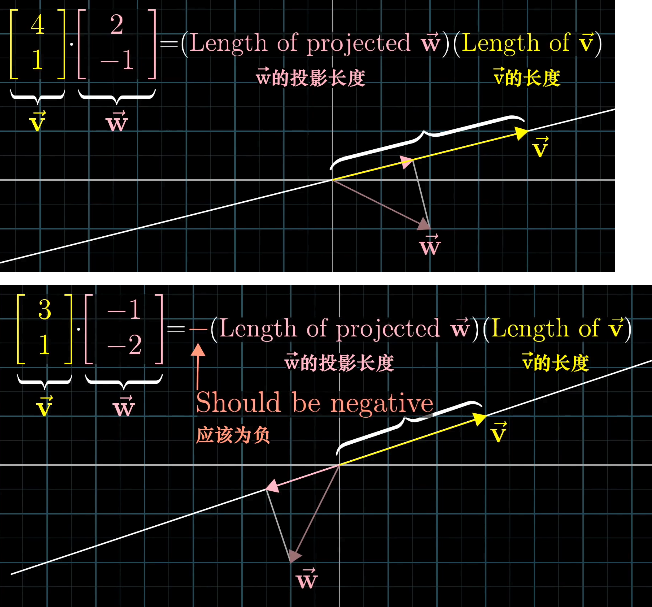
因此，点积常用于检查两个向量是否同向：

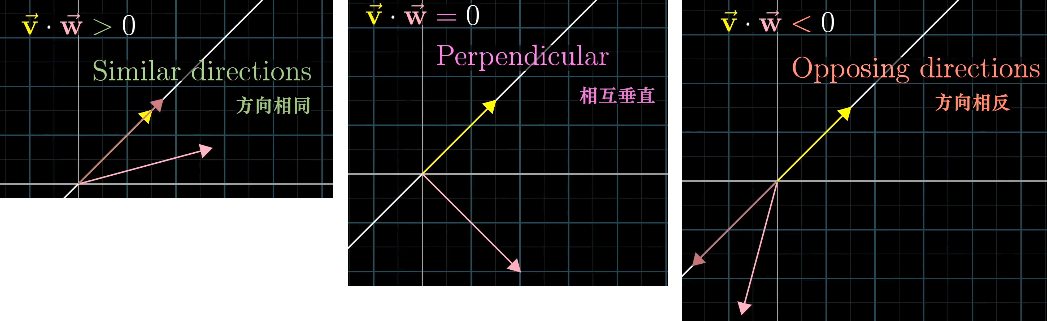
点积与向量顺序无关：

点积与向量顺序无关的证明：

1. 首先，假设向量$\vec{v}$与$\vec{w}$长度相等。那么，$\vec{v}$在$\vec{w}$上的投影与$\vec{w}$在$\vec{v}$的投影也相等。所以，向量顺序无关。
2. 然后，将$\vec{v}$缩放至$2\vec{v}$
   1. $(2\vec{v}) \cdot \vec{w}$等于$\vec{w}$在$\vec{v}$的投影乘以$2\vec{v}$，因为$2\vec{v}$等于$\vec{v}$的2倍，所以等于$2(\vec{v} \cdot \vec{w})$。
   2. $(2\vec{v}) \cdot \vec{w}$等于$2\vec{v}$在$\vec{w}$的投影乘以$\vec{w}$，因为$2\vec{v}$在$\vec{w}$的投影等于$\vec{v}$在$\vec{w}$的投影的2倍，所以也等于$2(\vec{v} \cdot \vec{w})$。

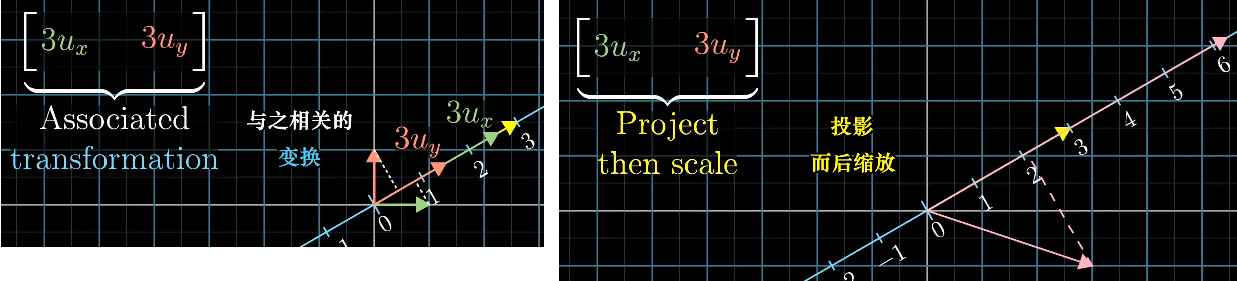
推导点积计算公式

1x2矩阵变换的计算公式与点积完全相同，1x2矩阵就像倾倒的向量。

1. 假设存在一个从2维空间到1维空间的变换，它的列空间是一条直线，变换的过程是向量向这条直线上做投影。这个变换符合线性变换，是1x2矩阵。
2. 在xy坐标系中，假设这条直线上的单位向量为$\vec{u}$，坐标为$(u_x, u_y)$。xy坐标系的基向量分别向这条直线作投影，得到变换后的基向量。
3. 因为$\vec{u}$为单位向量与基向量长度相等，所以变换后基向量为$u_x$、$u_y$，得到变换矩阵$[u_x \quad u_y]$。
   
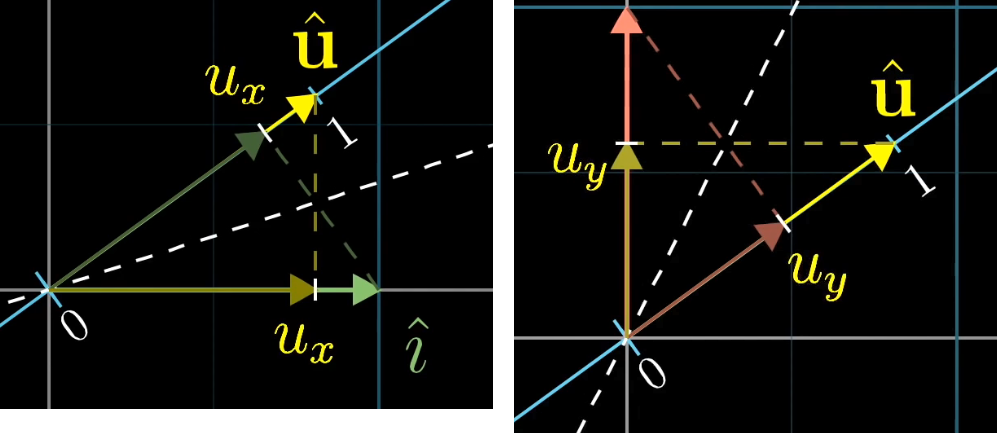
4. 因此，任意向量应用$[u_x \quad u_y]$变换的结果，是在$\vec{u}$上的投影，也是这个向量与$\vec{u}$的点积。
   
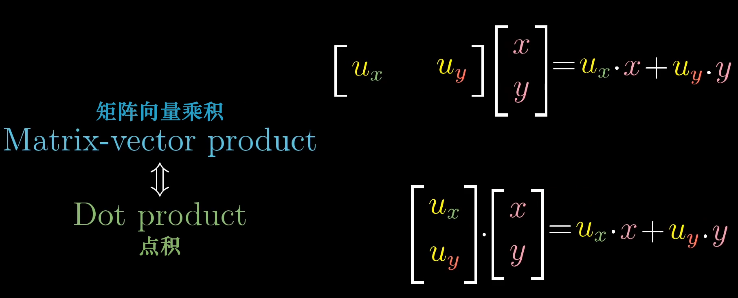
5. 当$\vec{u}$不为单位向量时，假设缩放为$3\vec{u}$。因为是线性变换，那么任意向量应用$[3u_x \quad 3u_y]$变换的结果，等价于先在$\vec{u}$上做投影，再缩放3倍，也就是这个向量与$3\vec{u}$的点积。