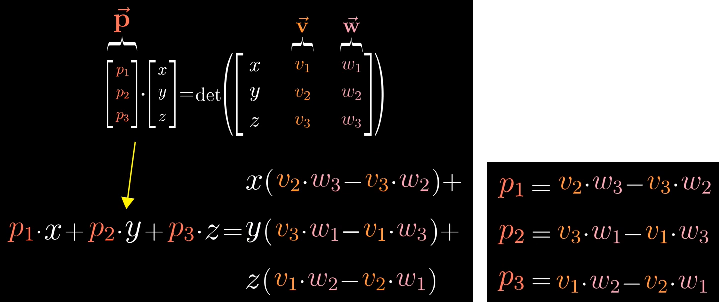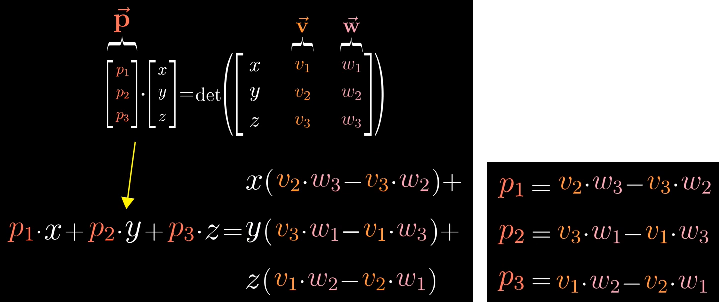Fly_Fire1000的博客

叉积的计算公式的推导：

1. 假设存在两个三维向量$\vec{v}$、$\vec{w}$，它们的叉积为$\vec{p}$，即$\vec{v} \times \vec{w} = \vec{p}$。并假设存在任意三维向量$(x, y, z)$。
2. $(x, y, z)$与$\vec{p}$的点积的绝对值，等于$(x, y, z)$在$\vec{p}$上的投影长度乘以$\vec{p}$的长度，如果$(x, y, z)$与$\vec{p}$同向，点积为正，反之为负。已知，$\vec{p}$的长度等于$\vec{v}$、$\vec{w}$围成的平行四边形面积。
3. 因为$\vec{p}$垂直于$\vec{v}$、$\vec{w}$，所以$(x, y, z)$与$\vec{p}$的点积绝对值等于$(x, y, z)$、$\vec{v}$、$\vec{w}$围成的平行六面体体积。
4. $(x, y, z)$、$\vec{v}$、$\vec{w}$围成的平行六面体体积，等于以它们为列向量的矩阵的行列式的绝对值。
5. 因为$\vec{p}$是$\vec{v}$、$\vec{w}$的叉积，列向量依次为$\vec{v}$、$\vec{w}$、$\vec{p}$的矩阵，变换后坐标系定向不会发生变化，行列式为正。
6. 因此，列向量依次为$\vec{p}$、$\vec{v}$、$\vec{w}$的矩阵，行列式也为正。
7. 因此，列向量依次为$(x, y, z)$、$\vec{v}$、$\vec{w}$的矩阵，如果$(x, y, z)$与$\vec{p}$同向，行列式为正，反之为负。
8. 因此，$(x, y, z)$与$\vec{p}$的点积等于列向量依次为$(x, y, z)$、$\vec{v}$、$\vec{w}$的矩阵的行列式。
9. 因此，叉积$\vec{p}$的计算公式如下：