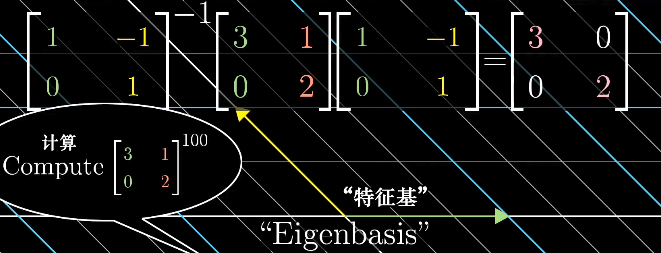
《P14 线性代数的本质 - 系列合集 10 - 特征向量与特征值》3Blue1Brown 笔记
一个线性变换,如果存在一个非零向量,变换后只进行了缩放,那么这个向量称为这个变换的特征向量,其中缩放的值就是特征值。
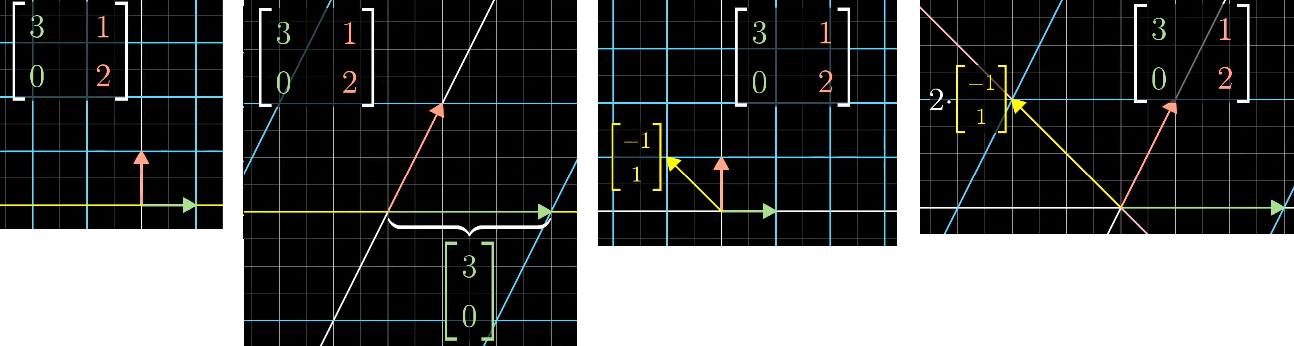
特征向量与特征值计算公式推导:
- 依据特征向量与特征值的定义,如下等式成立。
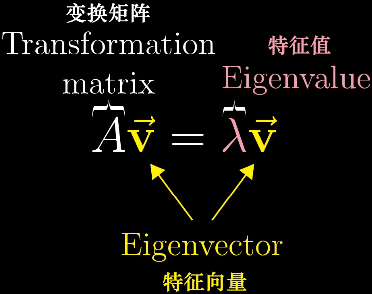
- 向量乘以特征值λ等价于,向量乘以一个缩放变换

- 将等式右边的部分移动到左边,得到一个变换矩阵,这个变换使特征向量变为零向量。
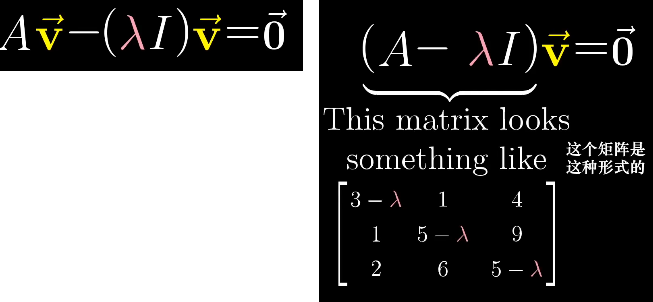
- 因为特征向量是非零向量,因此这个变换减少了空间的维度,它的行列式为0,代入行列式计算公式就可以推导出特征值的计算公式。
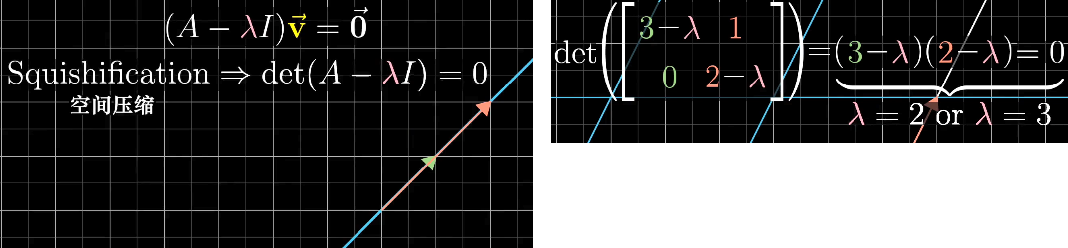
- 求出特征值,代入变换矩阵,矩阵的零空间就是特征向量。
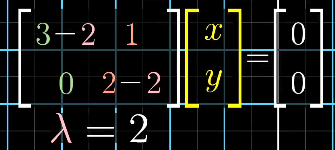
不同的线性变换,拥有特征向量、特征值的数量不同。
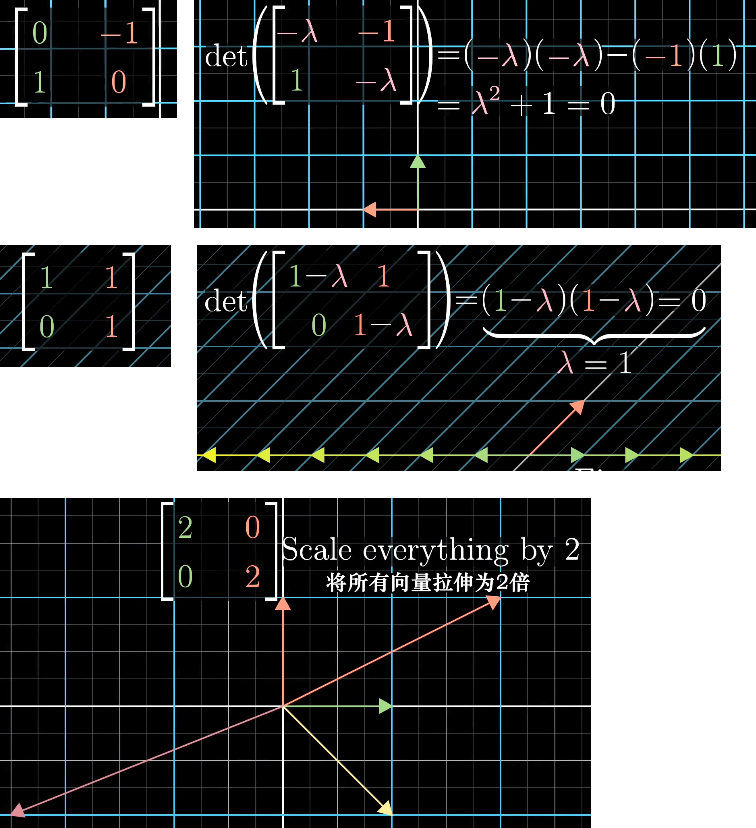
- 二维旋转变换,没有特征向量、特征值。
- 剪切变换,有无穷个特征向量(x轴),只有一个特征值。
- 缩放变换,有无穷个特征向量(整个空间),只有一个特征值。
只有对角线不是0的方形矩阵算为对角矩阵。对角矩阵在应用多次变换时,计算尤为便利。
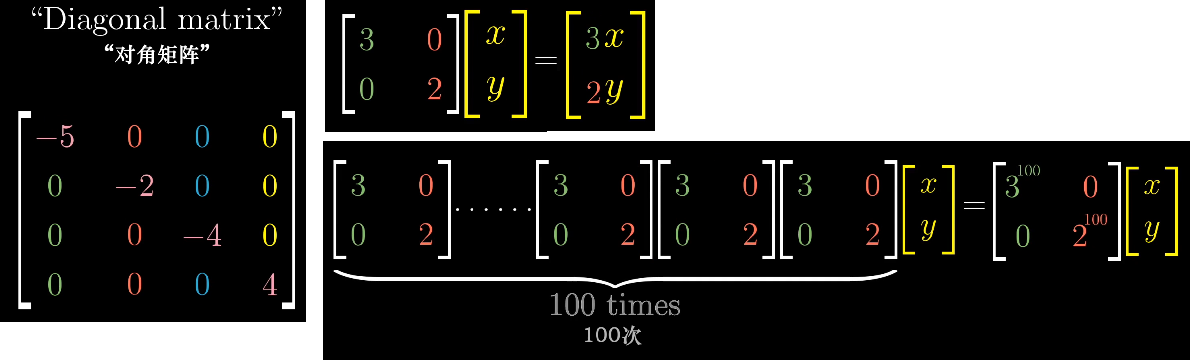
如果一个变换,当前使用的基的基向量恰好都是特征向量,变换后基向量只进行缩放,缩放值为特征值,这个变换显然是一个对角矩阵。
一个变换,当前使用的基的基向量恰好都是特征向量的情况并不多见。但如果一个变换的特征向量足够多,能找到一组特征向量张成的空间与这个变换的列空间维度相同。这个变换等价于先将这个变换使用的基变换为以这组特征向量为基,变换的矩阵变为对角矩阵,应用变换,之后将使用的基变换回原来使用的基。这样一组特征向量组成的基,称为特征基。