《P15 线性代数的本质 - 系列合集 11 - 抽象向量空间》3Blue1Brown 笔记
向量可以是函数,加法和数乘的意义如下:
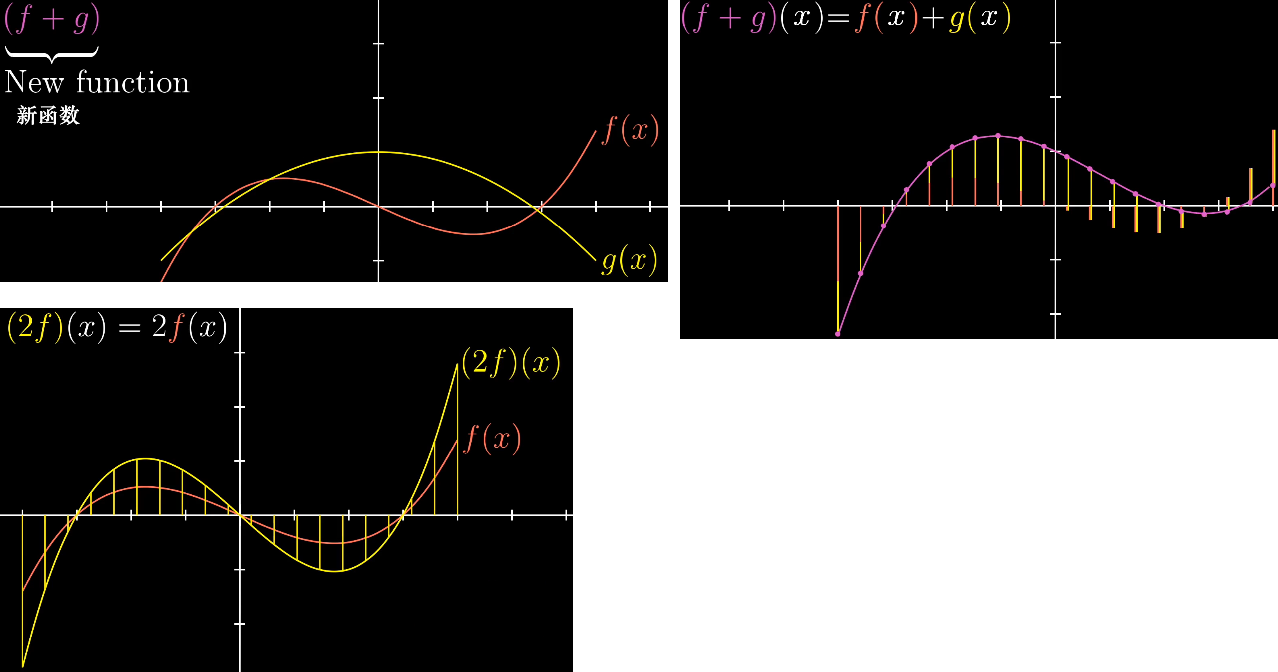
既然函数是向量,那么函数也能进行变换,下图的变换就是求导。
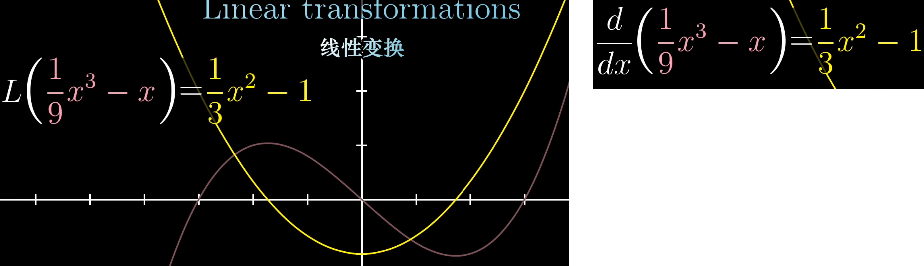
一个变换称为线性变换,泛用的定义如下:
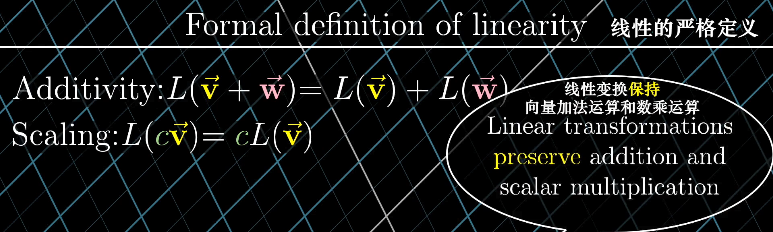
求导是线性变换。
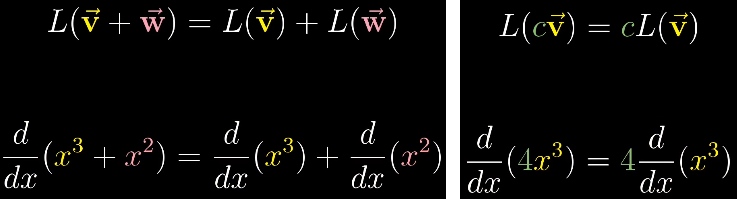
求导同样能被写成矩阵形式,在全体多项式空间中:
- 首先,确定基向量(基函数)。
- 然后,将多项式写成向量形式。
- 最后,将求导写成矩阵形式。
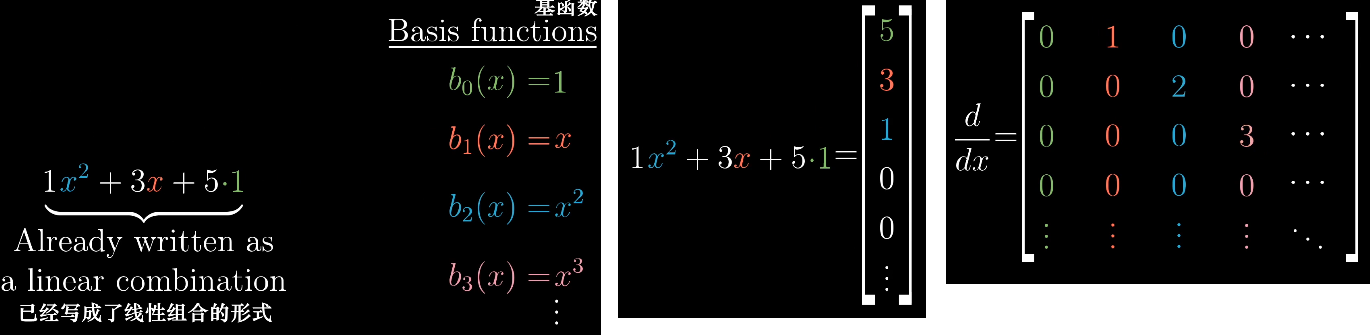
求导变换的验证如下:
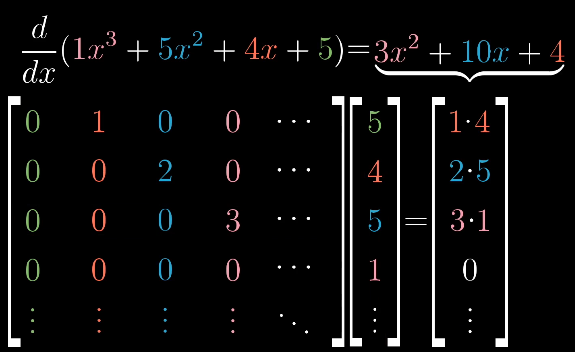
线性代数中的概念应用于函数时,名称稍有差异,但仍指的相同的事物。

向量加法与数乘的规则如下。

向量可以是任何事物,只要遵循这些规则,所有向量的概念都适用于它。这些事物的集合称为向量空间。