《P16 线性代数的本质 - 系列合集 12 - 克莱姆法则,几何解释》3Blue1Brown 笔记
克莱姆法则是一种线性方程组的解法,但不是最好的方法,不如高斯消元法。
已知解线性方程组可以转换为寻找一个目标向量,这个向量应用给定变换后为给定向量。
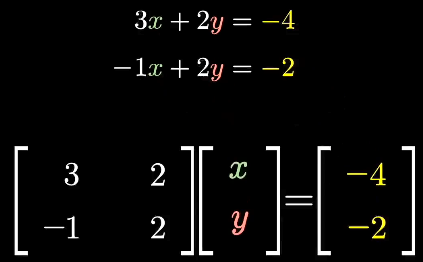
当变换矩阵的行列式为0时,空间维度减少,要么不存在目标向量,要么存在无数个目标向量。

本文只考虑行列式不为0的情况。
大部分变换前后,点积都会发生变化。
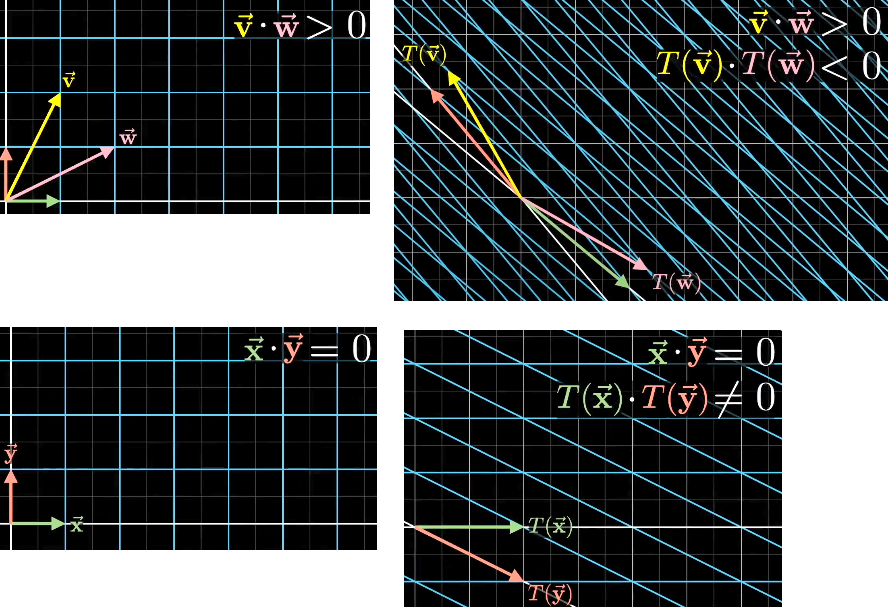
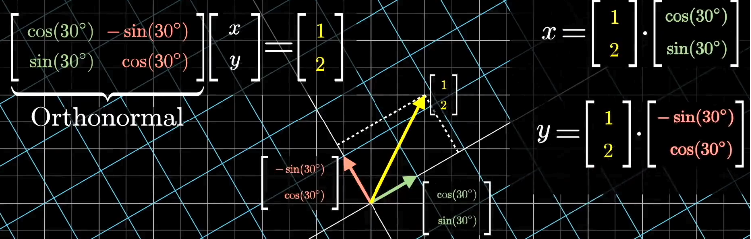
变换前后,点积不发生变化的变换,称为正交变换,如旋转变换。
如果给定变换是正交变换,那么点积不变,已知给定向量与变换后的基向量(变换矩阵的列向量)的点积,等于目标向量与变换前的基向量的点积,即目标向量对应轴上的坐标。
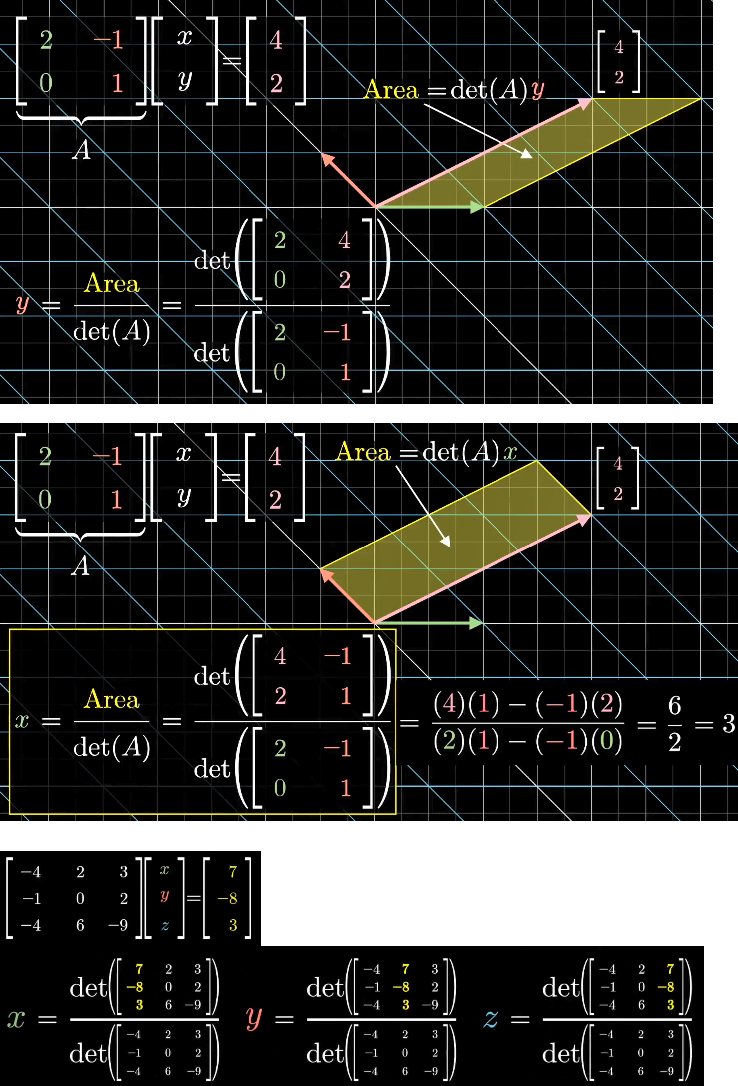
在二维空间中,向量在对应轴上的坐标分量等于这个向量与另一个轴上的基向量(长度为1)围成的平行四边形的有向面积,其中坐标分量为正时,面积为正,反之为负。这个有向面积又等于以这个向量和基向量为列向量的矩阵的行列式,调整这个向量和基向量的排列顺序,使得行列式与坐标分量同正负。
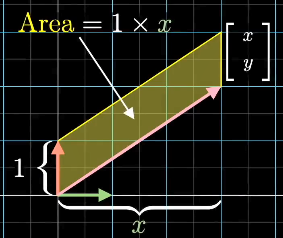
在三维空间中,因为两个基向量围成的面积为1,所以向量在对应轴上的坐标分量等于这个向量与其他两个轴上的基向量围成的平行六面体的有向体积,其中坐标分量为正时,体积为正,反之为负。这个有向体积又等于以这个向量和对应的两个基向量为列向量的矩阵的行列式,调整这个向量和两个基向量的排列顺序,使得行列式与坐标分量同正负。
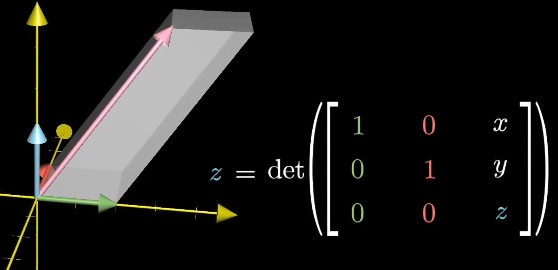
已知线性变换后,空间的缩放值等于这个变换的行列式。那么,无论是上文的平行四边形还是平行六面体,变换后的有向大小都等于原来的有向大小乘以这个变换的行列式。换句话说,将变换后的有向大小除于这个变换的行列式,就能得到目标向量的坐标分量。
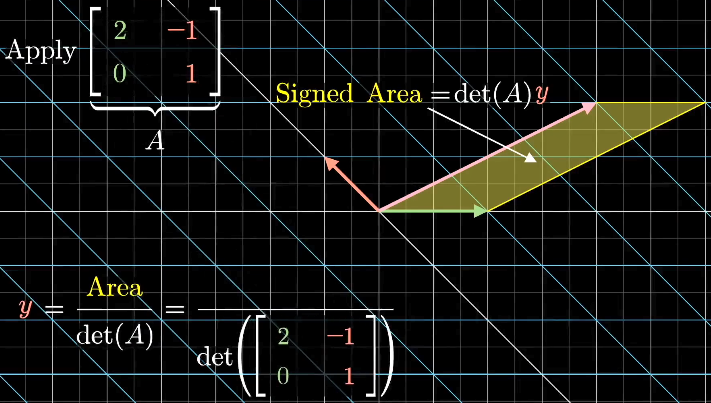
因为,变换后的向量,即给定向量是已知的。变换后的基向量,即变换矩阵的列向量是也已知的。所以,给定向量与变换后的基向量围成的平行四边形、平行六面体的有向大小也是已知的,等于以它们为矩阵的行列式。所以目标向量的坐标分量,即线性方程组的解的计算方法如下: